Модель Солнечной системы на vpython
Есть такая библиотека - vpython, с помощью нее можно создавать различные анимации и рисовать 3d объекты. Интересно было бы смоделировать хотя бы очень простую версию Солнечной системы. У меня не получилось сделать это самому, поэтому я нанял человека на upwork, чтобы он помог мне. Код в данном посте не мой, а этого человека, я лишь немного изменил его.
Сначала установим vpython:
pip3 install vpython
Попробуем нарисовать сферу:
1from vpython import sphere 2 3sphere()
Теперь, если все работает, начнем с того, что зададимся константами, нужными для дальнейших вычислений:
1from vpython import sphere, vector, color, rotate 2import math 3 4# Константы 5G = 6.667e-11 # гравитационная постоянная, м^3 кг^-1 с^-2 6MS = 1.9885e30 # масса Солнца, кг 7ME = 5.97e24 # масса Земли, кг 8MM = 7.348e22 # масса Луны, кг 9RSE = 1.496e11 # среднее расстояние от Солнца до Земли, метры 10REM = 384.4e6 # расстояние от Земли до Луны
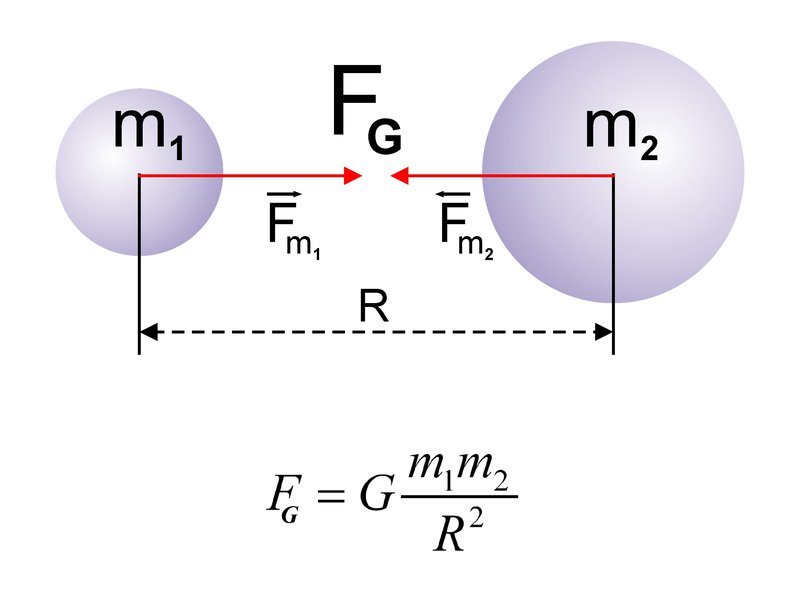
Далее вычислим гравитационные силы между Солнцем и Землей и между Землей и Луной по формуле:
$$F=G\frac{m1\cdot m2}{R^2}$$
1# Гравитационная сила между Солнцем и Землей, Н 2F_SE = G*MS*ME/(RSE*RSE) 3# Гравитационная сила между Землей и Луной, Н 4F_EM = G*ME*MM/(REM*REM)
Далее вычисляем угловые скорости и обычные по формулам
$$\omega=\sqrt{\frac{F}{m\cdot r}}$$
$$v=\omega\cdot r$$
1# Угловая скорость Луны 2wm = math.sqrt(F_EM/(MM*REM)) 3# Угловая скорость Земли 4we = math.sqrt(F_SE/(ME*RSE))
Далее рисуем сами сферы, которые будут представлять Солнце, Землю и Луну, конечно размеры не в масштабе для наглядности:
1v = vector(0.5, 0, 0) 2E = sphere(pos=vector(3, 0, 0), color=color.blue, radius=.25, make_trail=True) 3M = sphere(pos=E.pos+v, color=color.white, radius=0.08, make_trail=True) 4S = sphere(pos=vector(0, 0, 0), color=color.yellow, radius=1)
Потом, используя полярные координаты, обновляем позиции тел при каждом шаге:
1# Будем использовать полярные координаты 2# Шаг 3dt = 10 4# углы поворота за один шаг: 5theta_earth = we*dt 6theta_moon = wm*dt 7while dt <= 86400*365: 8 # Земля и Луна поворачиваются вокруг оси z (0,0,1) 9 Earth.pos = rotate(Earth.pos, angle=theta_earth, axis=vector(0, 0, 1)) 10 v = rotate(v, angle=theta_moon, axis=vector(0, 0, 1)) 11 Moon.pos = Earth.pos + v 12 dt += 10
Итого получилось:
1from vpython import sphere, vector, color, rotate 2import math 3 4# Константы 5G = 6.667e-11 # гравитационная постоянная, м^3 кг^-1 с^-2 6MS = 1.9885e30 # масса Солнца, кг 7ME = 5.97e24 # масса Земли, кг 8MM = 7.348e22 # масса Луны, кг 9RSE = 1.496e11 # среднее расстояние от Солнца до Земли, метры 10REM = 384.4e6 # расстояние от Земли до Луны 11# Гравитационная сила между Солнцем и Землей. Н 12F_SE = G*MS*ME/(RSE*RSE) 13# Гравитационная сила между Землей и Луной, Н 14F_EM = G*ME*MM/(REM*REM) 15# Угловая скорость Луны 16wm = math.sqrt(F_EM/(MM*REM)) 17# Угловая скорость Земли 18we = math.sqrt(F_SE/(ME*RSE)) 19 20v = vector(0.5, 0, 0) 21Earth = sphere( 22 pos=vector(3, 0, 0), color=color.blue, radius=.25, make_trail=True) 23Moon = sphere(pos=Earth.pos+v, color=color.white, radius=0.08, make_trail=True) 24Sun = sphere(pos=vector(0, 0, 0), color=color.yellow, radius=1) 25 26# Будем использовать полярные координаты 27# Шаг 28dt = 10 29# углы поворота за один шаг: 30theta_earth = we*dt 31theta_moon = wm*dt 32while dt <= 86400*365: 33 # Земля и Луна поворачиваются вокруг оси z (0,0,1) 34 Earth.pos = rotate(Earth.pos, angle=theta_earth, axis=vector(0, 0, 1)) 35 v = rotate(v, angle=theta_moon, axis=vector(0, 0, 1)) 36 Moon.pos = Earth.pos + v 37 dt += 10
Также, я сделал видео работы данного скрипта, по-моему, получилось неплохо:
