Блог питониста

Согласно распространенной истории, школьный учитель математики Гаусса был ленив. Чтобы чем-то занять детей на долгое время, а самому вздремнуть, он попросил их сложить числа от 1 до 100.

Гаусс быстро дал ответ: 5050. Так быстро? Учитель не поверил, но юный гений оказался прав. Складывать все числа от 1 до 100 - это для слабаков! Гаусс нашёл формулу:

$$\sum_{1}^{n}=\frac{n(n+1)}{2}$$

$$\sum_{1}^{100}=\frac{100(100+1)}{2}=50\cdot 101=5050$$

Как это у него получилось? Давайте попробуем разобраться на примере суммы от 1 до 10.

Первый способ: разбить числа на пары

Запишем числа от 1 до 10 в виде матрицы c двумя строками и пятью столбцами:

$$\left(\begin{array}{c}1&2&3&4&5\\ 10&9&8&7&6 \end{array}\right)$$

Интересно, сумма каждого столбца равна 11 или $n+1$. И всего таких пар чисел 5 или $\frac{n}{2}$. Получаем нашу формулу:

$$Число\ столбцов\cdotСумма\ чисел\ в\ стобцах=\frac{n}{2}\cdot(n+1)$$

Если нечетное число слагаемых?

Что, если сложить числа от 1 до 9? У нас не хватает одного числа для составления пяти пар, но мы можем взять ноль:

$$\left(\begin{array}{c}0&1&2&3&4\\ 9&8&7&6&5 \end{array}\right)$$

Сумма столбцов теперь равна 9 или ровно $n$. А количество столбцов? По-прежнему пять столбцов (спасибо нулю!), но теперь количество столбцов определяется как  $\frac{n+1}{2}$ ( y нас $n+1$ чиcел и вдвое меньше столбцов).

$$Число\ столбцов\cdotСумма\ чисел\ в\ стобцах=\frac{n+1}{2}\cdot n$$

Второй способ: увеличить вдвое и записать в две строки

Мы немного по-разному считаем сумму чисел в этих двух случаях.
Может быть, есть способ одинаково посчитать сумму для четного и нечетного количества слагаемых?

Вместо того, чтобы делать из чисел своеобразную «петлю»,  давайте запишем их в две строки, при этом количество чисел умножим на два:

$$\left(\begin{array}{c}1&2&3&4&5&6&7&8&9&10\\10&9&8&7&6&5&4&3&2&1 \end{array}\right)$$

Для нечетного случая:

$$\left(\begin{array}{c}1&2&3&4&5&6&7&8&9\\9&8&7&6&5&4&3&2&1\end{array}\right)$$

Видно, что в обоих случаях сумма столбцов равна $n+1$, а количество столбцов $n$.

$$Число\ столбцов\cdotСумма\ чисел\ в\ стобцах=n\cdot(n+1)$$

Но нам нужна сумма только одной строки, поэтому:

$$\frac{n\cdot(n+1)}{2}$$

Третий способ: сделать прямоугольник

Есть еще одно объяснение, давайте попробуем сложить крестики, допутим у нас есть крестики:

x

xx

xxx

xxxx

xxxxx

Как нам посчитать количество крестиков? Давайте добавим такое же количество ноликов:

x ooooo

xx oooo

xxx ooo

xxxx oo

xxxxx o

Похоже просто на другое представление второго способа — каждая последующая строка пирамидки имеет больше крестиков и меньше ноликов. Количество всех крестиков и ноликов — площадь прямоугольника.

$$Площадь=Высота\cdotШирина=n\cdot(n+1)$$

Но нам нужна сумма крестиков, поэтому:

$$\frac{n\cdot(n+1)}{2}$$

Четветрый способ: среднее арифметическое

Известно: $Среднее\ арифметическое=\frac{Сумма}{Количество\ членов}$
Тогда: $Сумма = среднее\ арифметическое\cdotКоличество\ членов$

Количество членов нам известно — $n$. А как выразить Cреднее арифметическое?

Заметьте, числа распределены равномерно. На каждое большое число приходится маленькое, расположенное на другом конце.

1 2 3, среднее 2

1 2 3 4, среднее 2.5

В этом случае среднее арифметическое -  это среднее арфиметическое чисел 1 и $n$, тоесть $Среднее\ арифметическое=\frac{n+1}{2}$

$$Сумма = \frac{n+1}{2}\cdot n$$

Пятый способ: интеграл

Все мы знаем, что определенный интеграл вычисляет сумму. Посчитаем сумму от 1 до 100 интегралом? Да, но для начала давайте хотя бы найдем сумму от 1 до 3. Пусть наши числа будут функцией y(x). Нарисуем картинку:

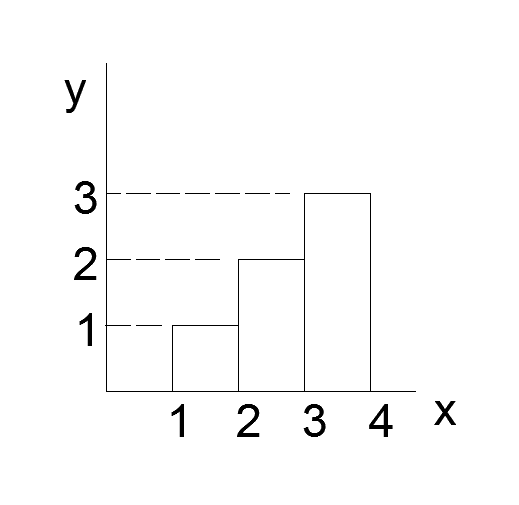
Высоты трех прямоугольников — как раз числа от 1 до 3. Проведем прямую через середины «шапок»:

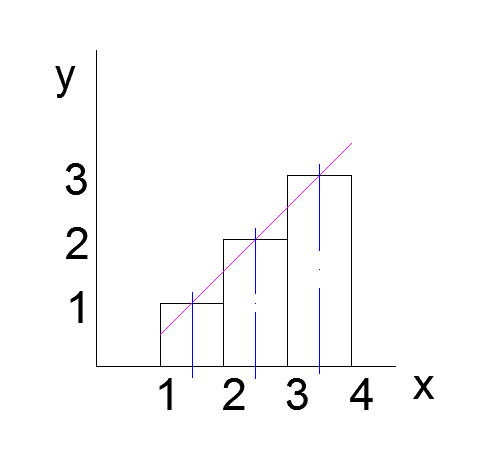
Неплохо было бы найти уравнение этой прямой. Она проходит через точки (1.5;1) и (2.5;2). $y=k\cdot x+b$.

$$\begin{cases}2.5k + b = 2\\1.5k + b = 1\end{cases}\Rightarrow k=1; b=-0.5$$

Таким образом, уравнение прямой, которой мы можем аппроксимировать наши прямоугольники $y=x-0.5$

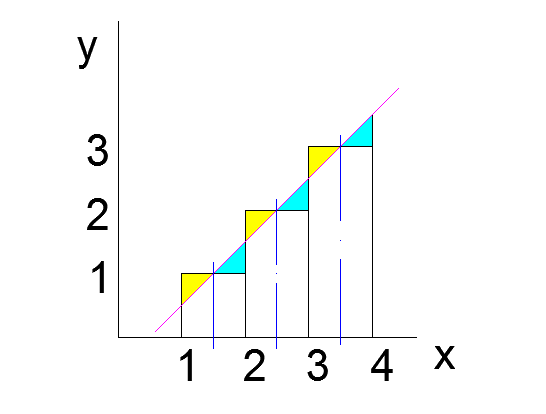
Она отсекает от прямоугольников желтые треугольники, но «добавляет» к ним сверху голубые. Желтые равны голубым. Сначала убедимся, что использование интеграла ведёт к формуле Гаусса:

$$\int_{1}^{n+1} (x-\frac{1}{2}) \, dx = (\frac{x^{2}}{2}-\frac{x}{2}){|}^{n+1}_{1}=\frac{(n+1)^{2}}{2}-\frac{n+1}{2}=\frac{n^{2}+2n+1-n-1}{2}=\frac{n^{2}+n}{2}$$

Теперь посчитаем сумму от 1 до 3, по иксу берем от 1 до 4, чтобы все наши три прямоугольника попали в интеграл:

$$\int_{1}^{4} (x-\frac{1}{2}) \, dx = (\frac{x^{2}}{2}-\frac{x}{2}){|}^{4}_{1}=\frac{4^{2}}{2}-2-(0.5-0.5)=6$$

Чтобы посчитать сумму от 1 до 100 нужно взять интеграл от 1 до 101:

$$\int_{1}^{101} (x-\frac{1}{2}) \, dx = (\frac{x^{2}}{2}-\frac{x}{2}){|}^{101}_{1}=\frac{101^{2}}{2}-50.5-(0.5-0.5)=5100.5-50.5=5050$$

И зачем все это нужно?

Наша формула позволяет быстро подсчитать сумму чисел. Заметьте:

$$\frac{n(n+1)}{2}=\frac{n^{2}}{2}+\frac{n}{2}$$

В первый день на ваш сайт зашел один человек, на второй день двое… Каждый день количество посещений увеличивалось на 1. Сколько всего посещений наберет сайт к концу 1000-го дня?

$$\frac{n(n+1)}{2}=\frac{n^{2}}{2}+\frac{n}{2}=\frac{1000^{2}}{2}+\frac{1000}{2} = 500000+500=500500$$

Данная статья — перевод с небольшим моим дополнением, оригинал.